[AI 이론] 자료 형태 (Data)
- AI & Data/이론
- 2022. 11. 2.

Data
최근 가장 핫한 기술인 AI는 Data를 기반으로 해요.
수많은 Data를 모으고, AI의 학습에 적합하게 전 처리하는 과정을 거치죠.
즉, AI를 활용하려면 Data를 다룰 줄 알아야한다는 뜻이죠.
그 시작으로 자료의 형태에 대해 알아볼게요.
자료 형태 구분

자료의 형태는 위와 같이 구분됩니다. 먼저 수치형 자료와 범주형 자료로 나눌 수 있어요.
수치형 자료에는 연속형 자료와 이산형 자료로 구분하고, 범주형 자료는 순위형 자료와 명목형 자료로 구분되네요.

좀 더 자세히 알아볼게요.
수치형 자료는 수치로 측정이 가능한 자료를 의미합니다. (키, 몸무게, 시험 점수, 나이 등)
반대로 범주형 자료는 수치로 측정이 불가능한 자료를 의미하죠. (성별, 지역, 혈액형 등)
여기서 주의할 점이 있어요.
수치형 자료와 범주형 자료의 구분을 자료를 숫자로 표현할 수 있는가로 생각하면 안 됩니다.
예를 들어볼게요.
- 범주형 자료가 숫자로 표현되는 경우
- 성별 구분: 남자 - 0, 여자 - 1
- 지역 구분: 서울 - 0, 경기 - 1, 인천 - 2, ...
- 수치형 자료를 범주형 자료로 변환하는 경우
- 나이를 연령대별로 Category화하는 경우 (10대, 20대, ...)
이렇게 구분된 데이터는 Machine Learning Algorithm도 다르게 적용됩니다.
범주형 데이터에는 "분류" 알고리즘이 적용됩니다.
수치형 데이터에는 "회귀" 알고리즘이 적용되죠.
각 알고리즘들은 "분류 한방에 끝내기(링크)"와 "회귀 한방에 끝내기(링크)"에서 다뤘으니 확인해보세요.
[AI Algorithm] 지도학습 - 분류 한방에 끝내기 (Classification / Ft. Decision Tree)
분류 개념 분류란? 분류는 주어진 입력값이 어떤 클래스(Label의 범주)에 속할지에 대한 결과 값을 도출하는 알고리즘입니다. 분류 알고리즘은 다양하게 존재하고, 예측 목표와 데이터 유형에 따
kay-dev.tistory.com
[AI Algorithm] 지도학습 - 선형 회귀 한방에 끝내기 (Linear Regression)
회귀 (Regression) 회귀 분석이란? 둘 이상의 변수가 있을 때 이들 간의 관계를 보여주는 통계적인 방법입니다. 나아가서 데이터를 가장 잘 설명하는 모델을 찾아 입력값에 따른 미래 결과값을 예측
kay-dev.tistory.com
범주형 자료
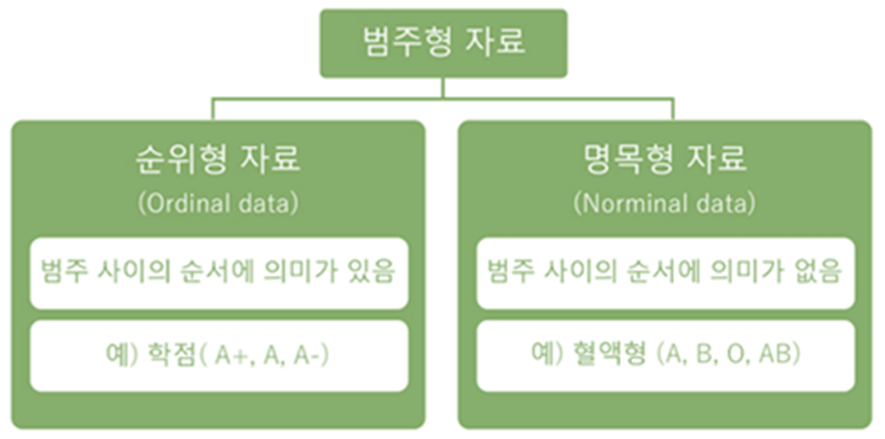
범주형 자료는 앞서 살펴본 것처럼 순위형 자료와 명목형 자료로 나눠집니다.
범주형 자료는 요약이 필요한데요, 다수의 범주가 반복해서 관측되거나 관측값의 크기보다 포함되는 범주에 관심이 있는 경우 때문입니다.
그럼 요약은 어떻게 하는지 알아볼게요.
범주 별로 관측값의 개수를 측정 ➡️ 전체에서 각 범주가 차지하는 비율을 파악 ➡️ 효율적인 범주간 차이 비교 가능
도수분포표 (Frequency Table)
도수란 "각 범주에 속하는 관측값의 개수"를 의미해요.
도수분포표란 "특정 구간에 속하는 자료의 개수를 나타내는 표"입니다.
도수(빈도수)를 바탕으로 도수분포표(Frequency Table), 상대 도수(Relative Frequency), 누적 상대 도수(Culmulative Relative Frequency)를 표현할 수 있어요.
도수분포표는 범주형 자료의 요약에 대표적으로 사용됩니다.
범주형 자료의 도수분포표는 각 범주에 속하는 관측값의 개수(빈도수, frequency)를 정리하여 놓은 것을 의미하죠.
상대 도수는 도수를 자료의 전체 개수로 나눈 비율을 의미해요.
누적 상대 도수는 측정값 순서대로 누적한 값을 뜻해요.
도수분포표에 대한 예시를 볼게요.


왼쪽은 설문조사의 결과를 나열한 표입니다. 아직 범주형 자료로 정리되기 전의 모습이네요.
이 결과를 "만족도"라는 범주로 구분해서 정리하면 오른쪽과 같은 표가 됩니다.
누적 상대도수는 특정한 기준으로 여러 범주들의 상대도수 합을 구하기 편한 장점이 있네요.
지금은 5가지라 와닿지 않을 수 있지만, 범주가 많아지면 확실히 편하겠죠?
이론만 보면 심심하니까 간단한 예제 코드를 보고 갈게요!
.value_counnts() # 도수
.value_counts(normalize=True) # 상대도수직접 사용해보면 아래와 같은 결과를 볼 수 있겠죠??
* 주의: csv 파일을 만들 때는 xlsx 파일에서 확장자만 바꾸면 안 됩니다!! 꼭 처음부터 csv 파일로 저장해주세요.


여기에 추가로 bar 차트까지 표현해볼게요.
import matplotlib.pyplot as plt
plt.bar(freq.index, freq.values) # 위에서 만든 freq 라는 data를 사용했어요.
plt.show
수치형 자료

이번엔 수치형 자료입니다.
수치형 자료는 연속형 자료와 이산형 자료로 구분되네요.
연속형 자료란 연속적인 관측값을 가지는 자료를 의미하고, 이산형 자료는 비연속적인 관측값을 가지는 자료입니다.

수치형 자료는 위와 같은 특징을 갖고 있어요.
이런 특징들이 있어서 대략적인 분포를 통계 값만으로도 알 수 있어요. 보다 쉽게 요약하고 파악할 수 있다는 뜻이죠.
요약에 대해 좀 더 자세히 알아볼게요.
평균, 분산, 표준편차가 등장합니다.

먼저 평균입니다.
평균은 관측값들을 대표할 수 있는 통계 값이죠. 그만큼 수치형 자료의 통계 값 중 가장 많이 사용됩니다.
하지만 극단적으로 크거나 작은 값에 영향을 많이 받는다는 단점이 있어요.
다음은 분산과 표준편차입니다.
데이터가 분포된 정도에 대한 값들이죠.
평균의 특성상 분포를 파악하기는 힘들죠. 그래서 데이터를 파악하기 위해 평균과 함께 사용됩니다.

위에 3가지 분포를 보면 평균은 같지만, 분산은 모두 다른 것을 볼 수 있습니다.
이때, A처럼 모여 있으면 분산이 작다. C처럼 넓게 퍼지면 분산이 크다고 표현해요.
분산에 대해 조금 더 볼게요.
분산은 자료가 얼마나 흩어졌는지를 숫자로 표현한 값입니다.
수학적으로는 "편차 제곱의 평균"이고, 각 관측값이 자료의 평균으로부터 떨어진 정도를 의미하죠.
아래와 같은 코드로 확인할 수 있어요.
from statistics import variance
variance(freq.values) # 분산표준편차는 분산의 양의 제곱근입니다.
왜 사용할까요??
분산의 단위는 "관측값 단위의 제곱"입니다. 즉, 관측값의 단위와 다르다는 뜻이죠.
그래서 표준편차를 이용해 관측값의 단위와 일치시켜 주는 역할을 합니다. (특성은 분산과 같아요.)
코드는 아래와 같습니다.
form statistics import stdev
stdev(freq.values) # 표준편차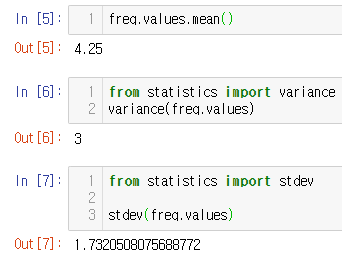
마지막은 히스토그램입니다.
히스토그램은 도수분포표를 그래프로 나타낸 것입니다.
형태는 막대그래프와 유사하지만, 다른 점이 있어요.
막대그래프는 y축에 대해서 주로 생각했다면 히스토그램은 x, y축을 모두 고려합니다.
코드와 예시를 보면서 이해해볼까요?
import matplotlib.pyplot as plt
plt.hist(freq.values) # 히스토그램
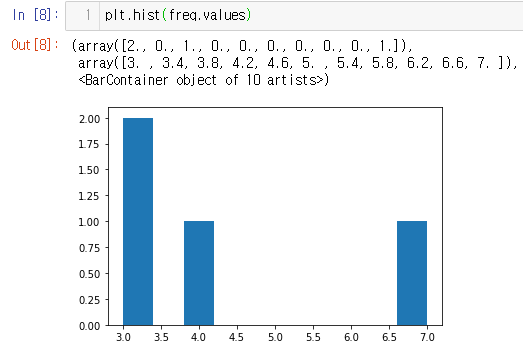

2번째 그림인 히스토그램은 x축에 data, y축에 data의 빈도수를 나타내고 있어요.
3번째 그림은 bar 차트로 x축엔 index, y축엔 data를 표현하고 있네요.
여기까지 "자료 형태"에 대해 알아봤어요.
다음에는 "데이터 전 처리"를 알아보겠습니다.
글이 도움이 되셨다면 공감 버튼 눌러주세요. 😊
'AI & Data > 이론' 카테고리의 다른 글
| [AI 이론] 활성 함수 한방에 끝내기 (Activation Function) (0) | 2022.11.10 |
|---|---|
| [AI 이론] 딥러닝 - 퍼셉트론 한방에 끝내기 (Perceptron) (0) | 2022.11.08 |
| [AI Algorithm] 지도학습 - 분류 한방에 끝내기 (Classification / Ft. Decision Tree) (0) | 2022.11.08 |
| [AI Algorithm] 지도학습 - 선형 회귀 한방에 끝내기 (Linear Regression) (0) | 2022.11.03 |
| [AI 이론] 데이터 전 처리 한방에 끝내기 (Data preprocessing feat.titanic) (0) | 2022.11.03 |